Quem agarra a ideia destes deliciosos sólidos platónicos?

Sólidos platónicos

Poliedros

Mandelbrot e os fractais

Mandelbrot, o criador da Geometria Fractal morreu com 85 anos em Cambridge, Massachusetts

O carbono 60, a bola de futebol e a igualdade de Euler

A 3 de Setembro a Google apresentava um banner celebrando os 25 anos da descoberta dos fulerenos por Robert F. Curl Jr., Sir Harold W. Kroto e Richard E. Smalley (esta descoberta valeu o Prémio Nobel da Química de 1996 a estes investigadores).

O que são fulerenos?

Fulerenos são  formas muito estáveis do carbono. Um dos fulerenos é o C60 designado por buckminsterfulereno em homenagem ao arquitecto Buckminster Fuller ( 1895-1983) pelas suas famosas estruturas - as cúpulas geodésicas.

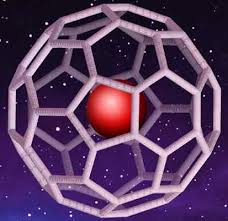Pela semelhança da sua estrutura com a de uma bola de futebol também se designa este alótropo do carbono por buckyball ou futeboleno.








Do icosaedro à bola de futebol

Truncando os vértices de um icosaedro chegamos ao poliedro que deu origem à bola de futebol.

A geometria da bola de futebol
Na bola de futebol há 60 vértices (V = 60) e 32 faces (F = 32). Como em cada vértice confluem 3 arestas, então há 90 arestas ( A = 3x60/2) (nota que cada aresta "conta" para dois vértices). Verifica-se aqui a igualdade de Euler (F + V = A + 2).


Quantas faces pentagonais há em qualquer fulereno?
Em qualquer fulereno cada átomo - vértice- está ligado a 3 outros átomos. O número de ligações - arestas - é então A = 3V/2 ou seja V = 2A/3.
Da igualdade de Euler vem que F + 2A/3 = A + 2 e obtemos F = A/3 + 2.
Mas num fulereno há P faces pentagonais e H faces hexagonais o que implica que:
F = P + H e A =(5P + 6H)/2 ( 5 arestas de cada pentágono e 6 arestas de cada hexágono, sendo cada aresta "partilhada" por duas faces).
Assim A = (5P + 6(A/3 +2 - P))/2 equação que resolvida dá P=12. Assim qualquer fulereno tem 12 faces pentagonais variando unicamente o número de faces hexagonais.
No caso do C60, cada pentágono está rodeado por um colar de cinco hexágonos. Se o número desses colares ao redor de cada pentágono for aumentado para 2, 3 ou mais, obtém-se uma família de fulerenos gigantes que começa com C240 e C540 (a família é dada por C60n2, onde n = 1, 2, 3 etc.).
Essas moléculas, à medida que se tornam maiores, ficam menos esféricas.


Para saber mais sobre a geometria dos fulerenos:
Romeu C. Rocha Filho, Os fulerenos e a sua espantosa geometria molecular, na revista Química Nova na Escola, nº4 de Novembro de 1996

From now to infinity

De This isn't hapiness

Mário Vargas Llosa e a Matemática

Mário Vargas Llosa, Prémio Nobel da Literatura 2010 escreveu em Pantaleão e as visitadoras
Parece que o quartel funcionou como um relógio graças a você. —
“Organizador nato, sentido matemático da ordem, capacidade executiva” — lê o Tigre
Collazos. — “Conduziu a administração do regimento com eficácia e verdadeira
inspiração.”

O mundo em 5 de Outubro de 1910

Comemora-se hoje o centésimo aniversário da Implantação da República. Mas, como era o mundo nesse tempo?

No desporto começavam as equipes de futebol e a competição - já é desse tempo a rivalidade entre o Porto e Lisboa!

Na Arte começa o pós-impressionismo. São desta altura
Matisse

George Braque

Amadeu Souza Cardoso


Na Literatura:
Teixeira de Pascoaes preparava a obra literária Marânus

Fernando Pessoa começa a escrever poesia e prosa


No pensamento destacam-se:
Raul Proença e António Sérgio (que defendeu que que a educação seria a causa directa do progresso)

Na tecnologia:
Começam a construir-se em série os primeiros carros

Blériot faz a primeira travessia aérea do Canal da Mancha


Na Arquitectura,
Ventura Terra e o Palacete Mendonça

Marques da Silva e o Teatro S. João no Porto

Na publicidade:

Nova edição da Enciclopédia Britânica é publicada contendo a obra de Darwin, Marx e Freud

Thomas H. Morgan inicia a investigação em Genética

Alfred Wegenel defende a deriva dos continentes

Russel e Whitehead publicam o primeiro volume de Principia Mathematica

Em Portugal destacam-se os matemáticos Aureliano Mira Fernandes e Francisco Gomes Teixeira

Bernardino Machado, presidente da I República também era licenciado em Matemática.

Na ficção científica assim se imaginava, em 1910, a escola do século XXI!!!!!